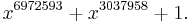Richard P. Brent

Richard Peirce Brent (b. 20 April 1946, Melbourne)[1] is an Australian mathematician and computer scientist, born in 1946. He holds the position of Distinguished Professor of Mathematics and Computer Science with a joint appointment in the Mathematical Sciences Institute and the College of Engineering and Computer Science at the Australian National University. From March 2005 to March 2010 he was a Federation Fellow[2] at the Australian National University. His research interests include number theory (in particular factorisation), random number generators, computer architecture, and analysis of algorithms.

In 1973, he published a root-finding algorithm (an algorithm for solving equations numerically) which is now known as Brent's method.[3]

In 1975 he and Eugene Salamin independently discovered the Salamin–Brent algorithm, used in high-precision calculation of \pi. At the same time, he showed that all the elementary functions (such as log(x), sin(x) etc.) can be evaluated to high precision in the same time as \pi (apart from a small constant factor) using the arithmetic-geometric mean of Carl Friedrich Gauss.[4]

In 1979 he showed that the first 75 million complex zeros of the Riemann zeta function lie on the critical line, providing some experimental evidence for the Riemann Hypothesis.[5]

In 1980 he and Nobel laureate Edwin McMillan found a new algorithm for high-precision computation of the Euler-Mascheroni constant \gamma using Bessel functions, and showed that \gamma can not have a simple rational form p/q (where p and q are integers) unless q is extremely large (greater than 1015000).[6]

In 1980 he and John Pollard factored the eighth Fermat number using a variant of the Pollard rho algorithm.[7] He later factored the tenth[8] and eleventh Fermat numbers using Lenstra's elliptic curve factorisation algorithm.

In 2002, Brent, Samuli Larvala and Paul Zimmermann discovered a very large primitive trinomial:

x^{6972593} %2B x^{3037958} %2B 1.

The degree 6972593 is the exponent of a Mersenne prime.[9]

He is descended from Hannah Ayscough, mother of Isaac Newton.

He is currently a Chief Investigator of the ARC Centre of Excellence for Mathematics and Statistics of Complex Systems.[10] He is a Fellow of the Association for Computing Machinery, the IEEE and the Australian Academy of Science. In 2005, he was awarded the Hannan Medal by the Australian Academy of Science.

References

  1. ^ Richard P. Brent "On the Precision Attainable with Various Floating-Point Number Systems"
  2. ^ Federation Fellowships Funding Outcomes 2004. Australian Research Council
  3. ^ Brent (1973). Algorithms for Minimization without Derivatives. Prentice-Hall, Englewood Cliffs, NJ. Reprinted by Dover Publications, Mineola, New York, January 2002. ISBN 0-486-41998-3.
  4. ^ Brent, R.P. "Multiple-Precision Zero-Finding Methods and the Complexity of Elementary Function Evaluation". Analytic Computational Complexity ed. Traub, J.F. (1975). Academic Press, New York.
  5. ^ Brent, R.P. (1979). "On the Zeros of the Riemann Zeta Function in the Critical Strip". Mathematics of Computation 33 (148) 1361-1372
  6. ^ Brent, R.P. and MacMillan, E.M. (1980). "Some New Algorithms for High-Precision Computation of Euler's Constant". Mathematics of Computation 34 (149) 305-312.
  7. ^ Brent, R.P. and Pollard, J.M. (1981). "Factorization of the Eighth Fermat Number". Mathematics of Computation 36 (154) 627-630.
  8. ^ Brent, R.P. (1999). "Factorization of the Tenth Fermat Number". Mathematics of Computation 68 (225) 429-451.
  9. ^ Brent, R.P. and Larvala, S. and Zimmerman, P. (2005). "A primitive trinomial of degree 6972593". Mathematics of Computation 74 (250) 1001-1002.
  10. ^ ARC Centre of Excellence for Mathematics and Statistics of Complex Systems Annual Report 2009

External links